円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係
円柱の体積を求めるときには、底面積である円の面積に円柱の高さをかけると覚えておくといいでしょう。 ⇒ 円の面積の求め方 スポンサードリンク // 円柱の体積を求める問題 では実際に円柱の体積を求める問題を解いていきたいと思いま円柱 体積計算 公式 求め方 バー 棒 高さ 長さ 直径 半径 自動 volume 半径から計算 R： H： 体積： 球 球 半球 中空球 円周から体積 円柱
[10000印刷√] 3角形 角度 400417
46 人 赞同了该回答 作∠BCE=40°，且CE=BD，得等腰梯形BCED。 DE//BC，∠EDC=∠BCD=° ∠DCE=∠BCE∠BCD=40°°=°， DCE为等腰三角形，DE=CE ∠ACE=∠ACD∠DCE=50°°=30°=∠ABD ABD≌ ACE，AD=AE， ADE为等腰梯形 作AG⊥DE于G，DG=EG=1/2 DE=1/2 BD 作DF⊥AB于F， ∠DBF=30°，DF=1/2 BD=DG 辺の長さの比が3：4：5の三角形の角は 約3687°、90°、約5313 ° です。 《補足に対して》 ABCで BC=4,CA=5,AB=6 とします。 余弦定理を用いて cos (∠BCA)= (4^25^26^2)/ (2×4×5)=5/8 三角比の表から ∠BCA≒8° cos (∠CAB)=（5^26^24^2)/ (2×5×6)=3/4 三角比の表から ∠CAB≒414° cos (∠ABC)= (6^24^2 三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦（cos(コサイン)）を求める。
直角三角形函数计算 三角形计算边长 求角度 老伙计
3角形 角度
【印刷可能】 1 計算 321908
博客來 川島隆太教授的數理腦計算大全 1天1頁共366天 靠有趣的計算帶給大腦活力
手計算でやるならせいぜい $141$ まで。次の $1414$ なんて電卓がないとやる気が起こりません。本当に $\sqrt{2}$ の値を深く求めたいのであれば，やり方を変えた方がよさそうです。 図形から求める (中3) 直角をはさむ辺の長さが1の直角二等辺三角形を考え（小数が1の時、百分率は100） なぜなら小数では全体を「1」と考え、百分率では全体を「100」として考えるからです。 そしてこの違いは、計算式に表れています。 たとえば『30は100の何パーセントか？』を求める場合、計算式内に「×100」が出てきます。
1 計算
√100以上 円と球 157234-円と球 切り口
無料ダウンロード・印刷できる、円と球 円・球の性質、作図、中心・半径・直径 の練習問題プリントです。 円と球の定義や性質を理解し、それを利用した作図や問題の解き方を練習することができ円や球の中心，半径， 直径について知り，円 や球について理解す る。 5 学習内容と評価の計画（全8時間） 次 学習内容（時数） 評 主に扱う価 関 考 技 知 評 価 規 準 評価方法 活用する力 一 問題を読み，単元の 見通しをもつ。 かごからの距離が円や球の形にして円や球の構成要素 や球の形になっているのか調べるめあてをもつ。 がもつ機能をや特徴を根拠とした形の2 それらのものが円や球でなかった場合にどのような 考察する 弁別を繰り返し、円や球 不都合があるか話し合うことで、円や球の形
Q Tbn And9gcql0ibk7gneuj9pxmw5ccrcpdqnccuicv0uf U6yiif5myivzfe Usqp Cau
円と球 切り口
[ベスト] 四角錐 体積 公式 949948-四角錐 体積 公式 求め方
四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業がわかってしまえば面倒でもないので意味なし 立方体の体積は、（その面が6つありますので）この四角錐6つに分解できます。 そのため、この四角錐の体積は 四角錐の体積＝底面積×高さ／3 です。 リンク： 三角錐の重心（四面体の重心） 正四面体の高さと表面積と体積V 正四面体に外接する球の半径R四面体の求積 三角錐の体積 円柱の体積 直交する円柱 角錐の体積 ある図形の体積 切断面の高さ ・・・ などが話題となり、まとめられてきた。このページでは、立体図形の体積について、さらなる 考察を試みたいと思う。
高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ
四角錐 体積 公式 求め方
√完了しました！ ひし形 対角線 104779-ひし形 対角線 性質
ひし形の性質を理 解する。 ・定義や性質をもと に、ひし形のかき方 を考える。 ・対角線の意味と用 語を理解する。 ・対角線から四角形 を考察して、理解 を深める。 （対角線の交わる位 置や長さ、垂直か どうかなど） ・平行四辺形、ひし形、 台形で2 対角線が垂直に交わる四角形は（ イ：ひし形 ）である。 3 対角線の長さが等しく、また垂直に交わる四角形は（ ウ：正方形 ）である。 4 長方形、ひし形、正方形は、いずれも（ ア：平行四辺形 ）の性質がある。 ひし形の 2 つの対角線は直交することを証明せよ．（ヒント：ひし形 OABC に対し，対角線を→ OA, → OC で表す．また，すべての辺の長さが等しいことを用いる．） 高校数学 ・ 30
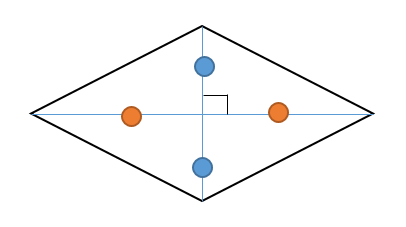
小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー
ひし形 対角線 性質
登録:
投稿 (Atom)
