無料ダウンロード・印刷できる、円と球 円・球の性質、作図、中心・半径・直径 の練習問題プリントです。 円と球の定義や性質を理解し、それを利用した作図や問題の解き方を練習することができ円や球の中心,半径, 直径について知り,円 や球について理解す る。 5 学習内容と評価の計画(全8時間) 次 学習内容(時数) 評 主に扱う価 関 考 技 知 評 価 規 準 評価方法 活用する力 一 問題を読み,単元の 見通しをもつ。 かごからの距離が円や球の形にして円や球の構成要素 や球の形になっているのか調べるめあてをもつ。 がもつ機能をや特徴を根拠とした形の2 それらのものが円や球でなかった場合にどのような 考察する 弁別を繰り返し、円や球 不都合があるか話し合うことで、円や球の形
Q Tbn And9gcql0ibk7gneuj9pxmw5ccrcpdqnccuicv0uf U6yiif5myivzfe Usqp Cau
円と球 切り口
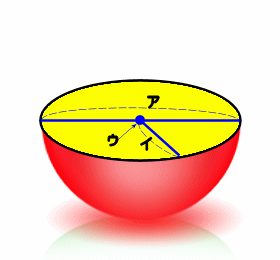
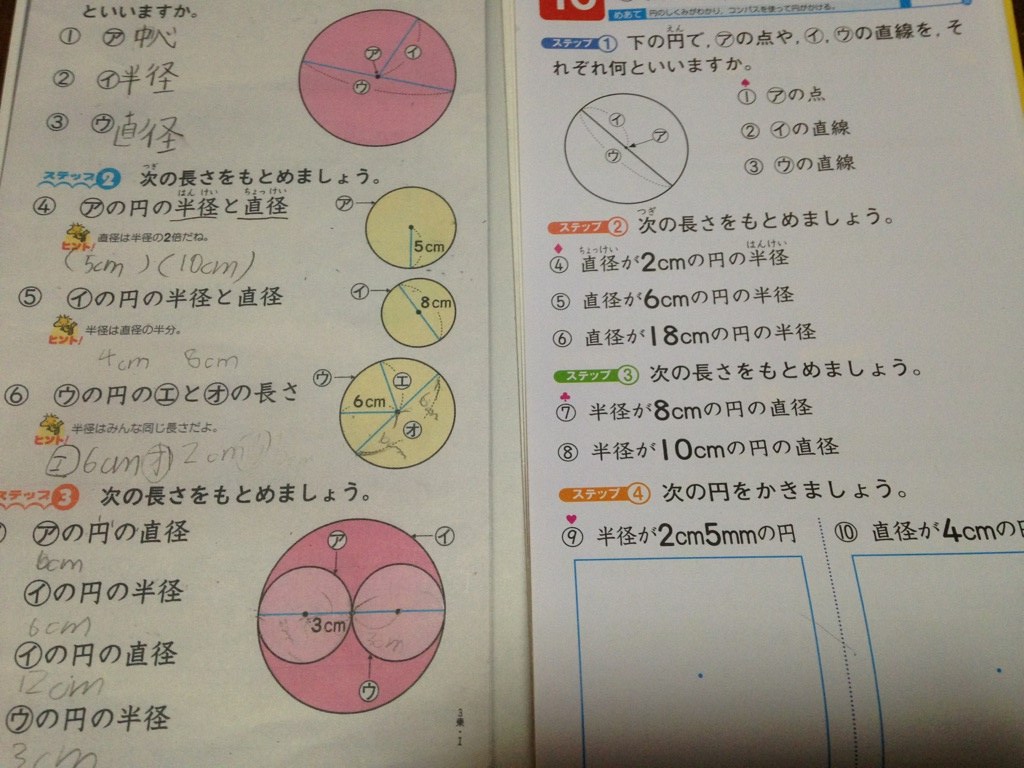
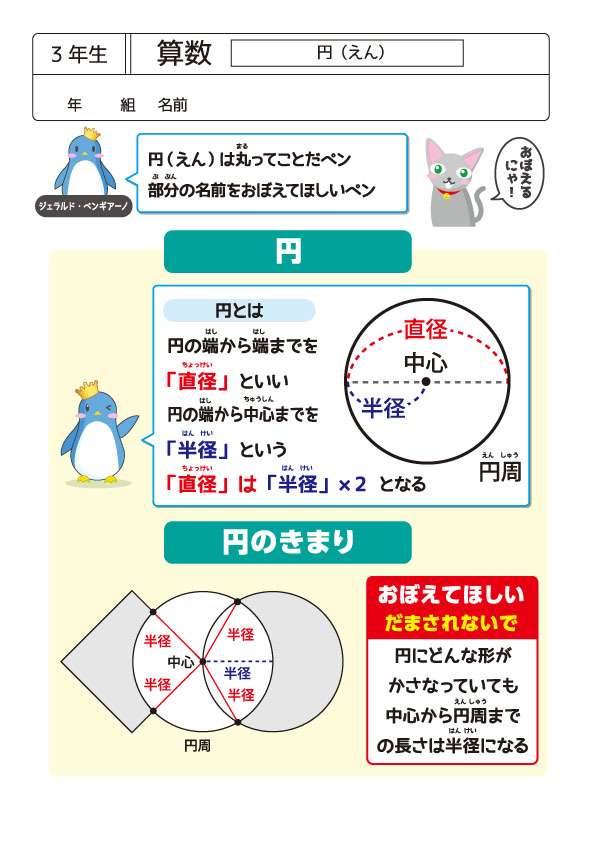
円と球 切り口-円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体球にも、円と同じで、中心や半径、直径があります。 球を半分に切った時の切り口の円の中心、半径、直径がそれ ぞれ、その球の中心、半径、直径になります。 の半 径や直 も、円 と 同じで何本 ひくこ球 が きま すし 長さ いつ 。 半径 中心 直径 はんけい



円と球 ドリル 児童デイサービスの学習支援
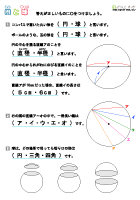
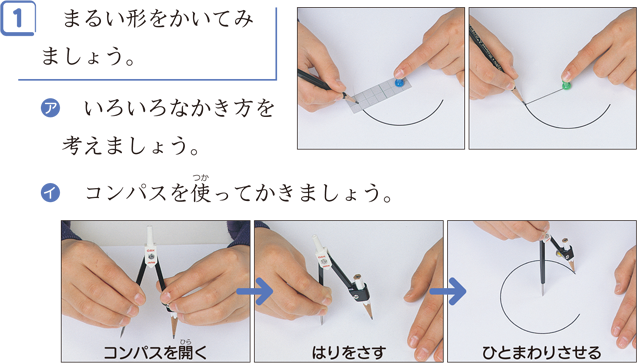
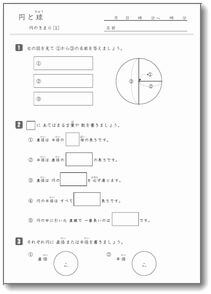
円と球 ① 月 日 名前 の中にあてはまることばを書きましょう。 1つの点から長さが同じになるように かいたまるい形を, といいます。 その1つの点を円の といい, 円のまわりまで引いた直線を, といい 学習のポイント 円や球の定義や性質、それぞれのもつ構成要素の関係を理解し、円と球の共通性を理解しましょう。 半径がみな等しく、直径=半径×2であることを理解しましょう。 コンパスを使って、指定された長さを正確に写し取りま・円の定義、円の性質、円の作図 ・直径と中心の関係 ・コンパスの使い方 ・球の概念と性質 小学生・中学生が勉強するならスクールtv。全国の学校の教科書に対応した動画で学習できます。授業の予習・復習にぴったり。
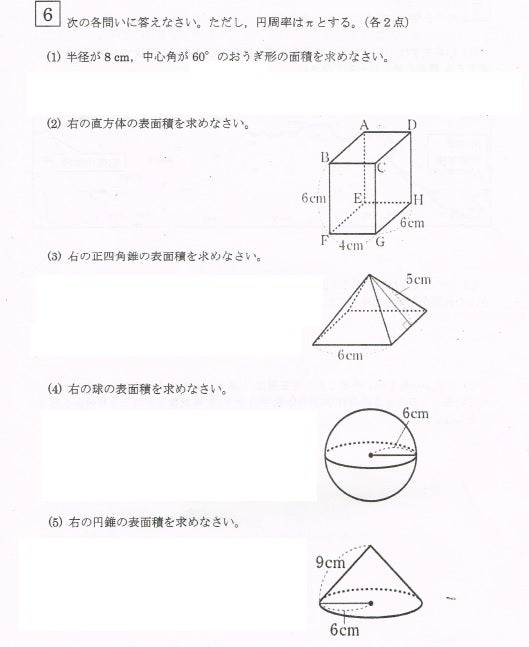
問題 下の図のように、底面の半径が \(28cm\),母線の長さが \(100cm\) の円錐に 球が内接しています。この球の半径を求めなさい。 解説 平面における、「三角形と内接円の関係」とほぼ同じです。 空間円,球について知ること。また,それらの中心,半径,直径について知ること。 本単元「円と球」 ・円や球についての観察や構成などの活動を通して,円や球を構成する要素に着目し,円や球 について理解できるようにする。 次単元「三角形と角」円や球についての理解や構成などの活動を通じて,円と球を構成する要素に着目し,円や球につ いて理解できるようにする。 4 単元の評価規準 算数への 関心・意欲・態度 数学的な考え方 数量や図形についての 技能 数量や図形についての 知識・理解
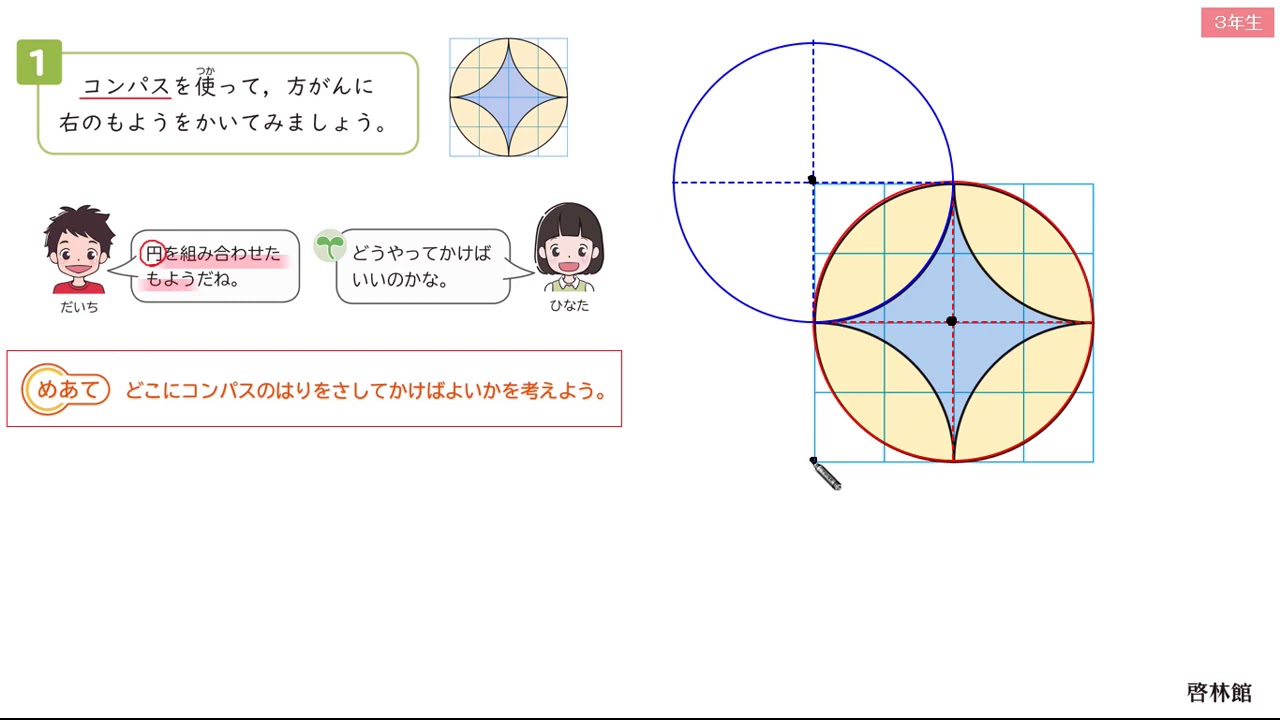
円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p円は中心の位置と半径の長さによって決まることをもとに,円の性質や機能につ いて考える。 (数学的な考え方) 球を平面で切った切り口が円になることから,球の概念を円と関連づけてとらえる。 (数学的な考え方)3年算数円と球 (1)わかる教え方コンパスの使い方 ①円や球の共通の性質の理解 ②円のかきかたとコンパスの使い方 ③円や球の中心・半径・直径の意味 ④円を使ったいろいろな模様づくりの楽しさ




3年生 算数 円と球 授業力アップ 学級経営の話
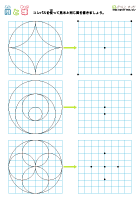



円と球プリント ぷりんときっず
・球の特徴を円と関係付けて 理解させる。 「課題の設定」の充実 ・球がぴったり入った箱の大きさの求め方を考える。 資・能② 思考力・判断力・表現力 考 円や球の性質を活用して,箱の大きさの求め方を考え,図や式を 使って説明している。 円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円・円と球の区別が 「円と球 指導案 ダウンロード 学年 第4学年 単元名 「いろいろな四角形」 家を建てる 指導案 ダウンロード 学年 第4学年 単元名 「面積」 指導案 ダウンロード 学年 第6学年 単元名 「どんな面積も求められる!~図形や式を変形させ




円と球 スクールプレゼンター教材共有サイト スクプレ道場



円と球 ドリル 児童デイサービスの学習支援
円や球に関心をも ち、身の回りから円 や球を見つけ、それ らが使われる場面 について考えよう とする。 円は、中心から等距離にあ る点の集まりであること を見出し、円は半径の長さ によって決まることにつ いて考え、表現することが できる円と円の間に存在する空間の割合は 93%。 上式中に \(a\) は含まれない。 すなわち,円の大きさに関係せずに空間の割合が決まる。 球と球の間の空間 同じ大きさの球を図 3 のように並べる。 図 3 その上に同じ大きさの球を図 4 のように乗せる。 図 4円の特徴に関心をもち,円の特徴を生かしながら様々な模様を作ろうとしている。 〔数学的な考え方〕 半径がみな等しいこと,直径が半径の2倍であることなどの特徴が全ての円や球で言え るかどうかを考えることができる。 〔技 能〕




Iq1 小3 公文の先取り学習と 算数 円と球の問題 子供の中学受験 24年




円と球 算数用語集
The latest tweets from @entokyu_円や球についての観察や構成などの活動を通して、円や球を構成する要素に着目し、円や球について理解でき るようにする。 (2)評価規準 関心・意欲・態度 数学的な考え方 技能 知識・理解 円や球に関心を持ち、身 の回りから円や球を見つ 球の表面積・・・4πr² r³を微分すると3r²になります。 つまり、球の体積を微分すると円の表面積の公式になります。 そもそも微分とは、『少しの増加の間の変化量』を表現しています。 円の面積のちょこっとの増加分は円の周りの長さに相当します。




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




L6nwuojodhgstm
温故知新ラーニングです。 今日から10月。 センター試験出願は10月10日(木)締切です! 個人出願の受験生は特に気をつけてください! さて、今回は数学。「円」と「球」についてです。た円の面積や球の体積・表面積を求めるための公式と して生徒は受け止め,これらの式を暗記すればよいと みる傾向が強い。 円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデ球 きゅう sphere 定点Cから等距離 r にある空間内の点全体の集合をいう。 Cを球の中心,r を半径という。 球はまた,円を直径のまわりに1回転して得られる回転面と考えてもよい。



Www Pref Kanagawa Jp Documents Monndai11 Pdf



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S3 013 Pdf




3年算数 円と球 まるい形をかいてみよう Youtube




円と球 スクールプレゼンター教材共有サイト スクプレ道場



3年の 円と球 でソフト 横山験也のちょっと一休み




ヨドバシ Com 小学3年生 5の巻 円と球 算数の壁をすらすら攻略 全集叢書 通販 全品無料配達




Newton 図形に強くなる 身近な円と球 By 科学雑誌newton




円と球プリント ぷりんときっず Pattern Flower Patterns Print
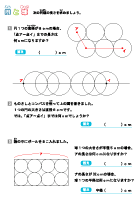



円と球プリント ぷりんときっず




小3算数 11 円と球1 教下p4 5 Youtube




画像 3年生 算数 円と球 プリント シモネタ
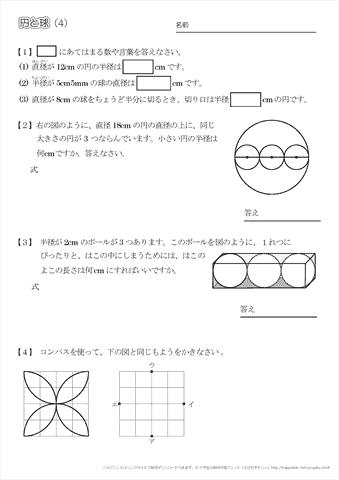



小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生



3年算数円と球 1 わかる教え方コンパスの使い方




算数プリント3年生 円と球
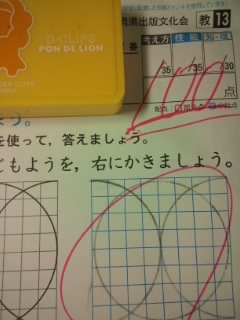



円と球のテスト L イベント大好き




円と球プリント ぷりんときっず



Www Pref Saitama Lg Jp Documents 3 11entokyu Mondai Pdf




小学校3年算数 02 3 円と球 きゅう Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト




円と球 きゅう Ict教材eboard イーボード
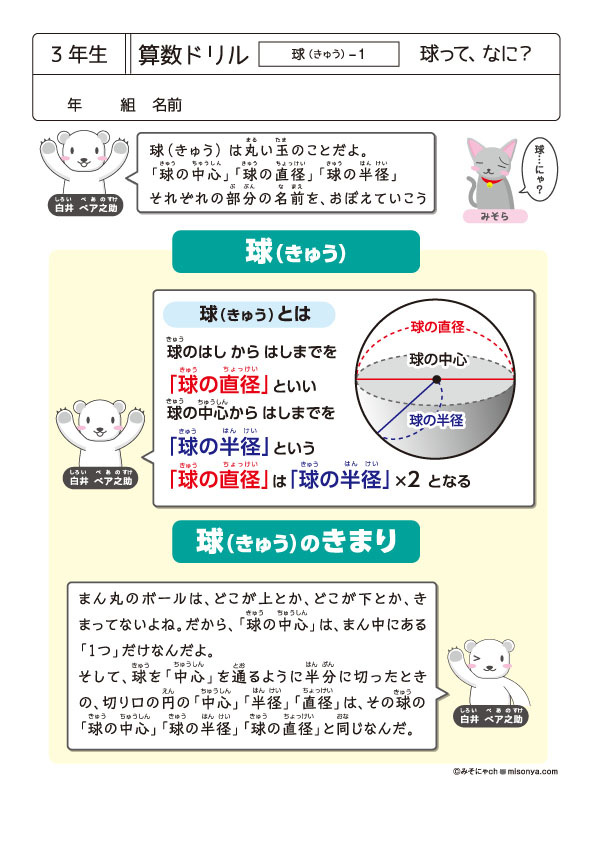



無料の学習プリント 小学3年生の算数ドリル 球 みそにゃch



みんなの算数オンライン 教科書レベル 2年 形と名前 円と球の形と名前 トレーニング




算数3年 の記事一覧 すきるまドリル 無料学習プリント
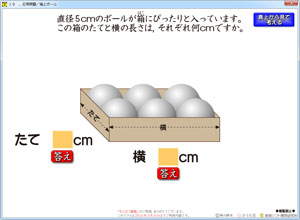



3年 円と球のソフト さくら社
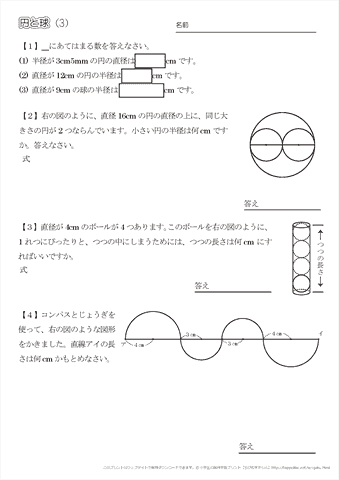



小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生



Q Tbn And9gcql0ibk7gneuj9pxmw5ccrcpdqnccuicv0uf U6yiif5myivzfe Usqp Cau



円と球 どうすればお宝の場所がわかるだろうか 館山市立北条小学校 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
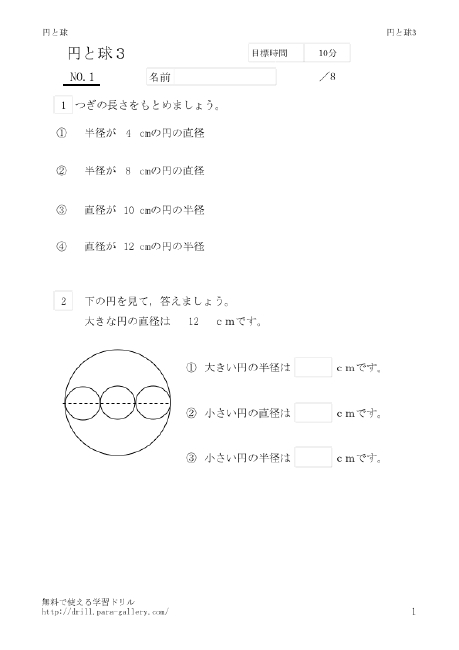



円と球




3年算数 円と球 円の中心を見つけよう Youtube



円と球の名前 2



円と球プリント ぷりんときっず



無料ダウンロード 小学校 3年生 算数 円と球 ニスヌーピー 壁紙




すきるまドリル 小学3年生 算数 円と球 無料学習プリント すきるまドリル 無料学習プリント



Cms Gakko Akiota Jp Kakesho Wysiwyg File Download 1 753




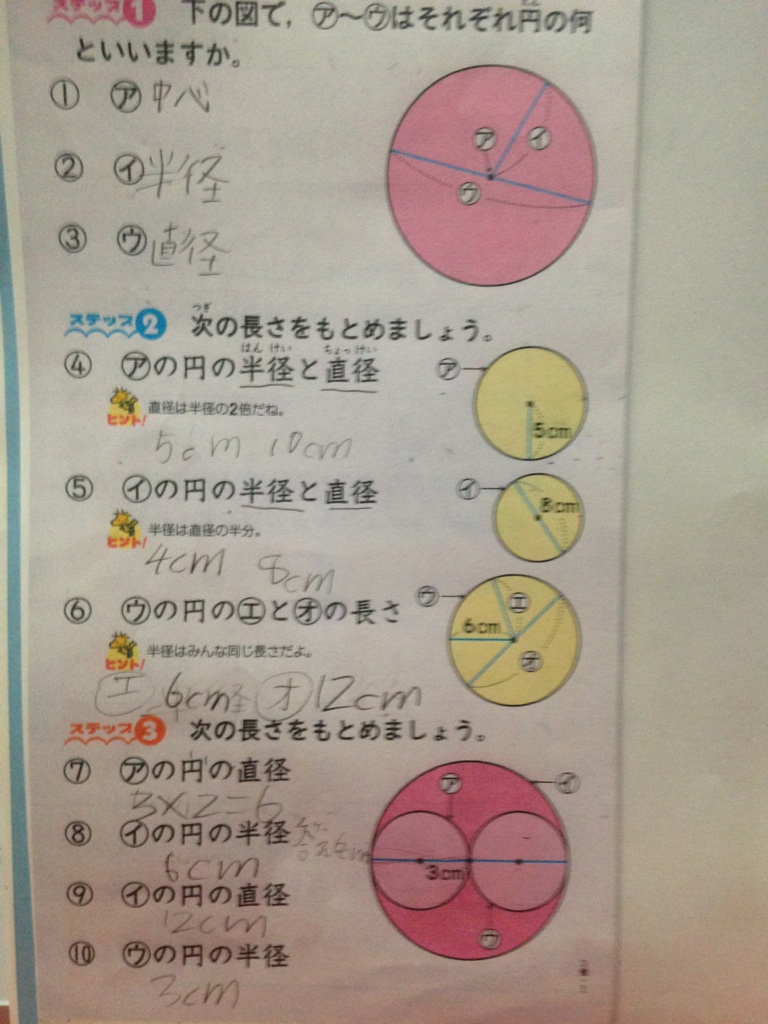
Tossランド 円と球 第2時 直径



2



家庭学習 次男小3 円と球 最終章 終わった ヘタレですが 2人の男の子育児中



Ss円と球 Ss304 2 幼児 小学生教材のエジソンクラブ 通販 Yahoo ショッピング




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



円と球 01 もようづくり Youtube




実践記録算数3年




円と球 低学年の無料学習ドリル



Http Www Edu Tens Net Syohp Murehp Kyuukou Purinto Pridata 3nen 3san3 Pdf




円と球 小学3年生 算数 5 二宮先生 Youtube




メルカリ 円と球の説明 知育玩具 1 300 中古や未使用のフリマ




小学3年生算数 円と球 もちおあかでみー Youtube




世界一分かりやすい算数 小3 円と球
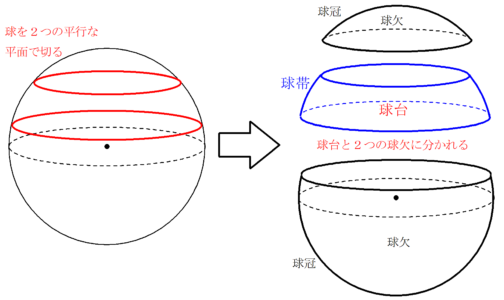



球台と球帯 Fukusukeの数学めも



円と球 算数用語集



小3算数 計算ドリル かけ算 わり算 円と球 1学期 By Keiko Suzuki



円と球から性教育に Honeypoo Note



Www City Adachi Tokyo Jp Documents Em 3 9 Pdf



堺市立野田小学校 のホームページ



1




三年生 算数 円と球 Noriko アカンパニスト




円と球プリント ぷりんときっず



3年算数円と球 3 わかる教え方のポイント



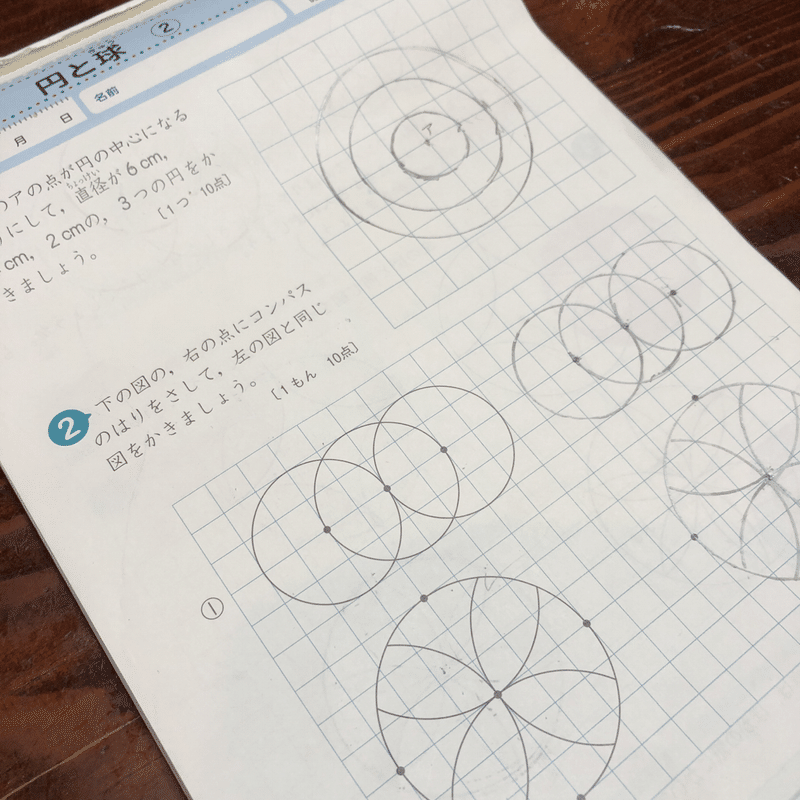
円と球プリント ぷりんときっず




3年算数円と球 3 わかる教え方のポイント



円と球 おうぎ形と円すい セルモ大蔵 世田谷 の塾長ブログ



Kyosys Open Ed Jp Multidatabases Multidatabase Contents Download 10 8da791f70e3874df438ad69 4625 Col No 15 Frame Id 16




小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生



算数イメージ動画集 大日本図書



2




世界一分かりやすい算数 小3 円と球




小学3年生 算数 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




円と球 算数の壁をすらすら攻略 本 通販 Amazon



小学3年生向けの円と球について学ぶ基本問題



小3算数 計算ドリル かけ算 わり算 円と球 1学期 By Keiko Suzuki




小3 算数 小3 9 球について Youtube




円と球 01 球 Youtube



家庭学習 次男小3 円と球 円 まずいです ヘタレですが 2人の男の子育児中



Schit Net Kasukabe Estakesatonishi Cabinets Cabinet Files Download 62 9bbbdb3104bf7e1a358 Frame Id 67




世界一分かりやすい算数 小3 円と球



2




世界一分かりやすい算数 小3 円と球




円と球 Youtube




小4算数 円と球 風車 ブログ アビット



2



堺市立浜寺昭和小学校 のホームページ




円と球 Entokyu Twitter




Tossランド 円と球 第6時 球



円と球 どうすればお宝の場所がわかるだろうか 館山市立北条小学校 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



円と球 愛パパ日記



2



1



Www City Hadano Kanagawa Jp Www Contents Simple C007 Pdf



1



Http Www Pref Osaka Lg Jp Attach 6629 H Emw Pdf
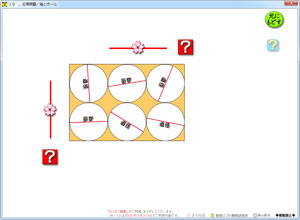



3年 円と球のソフト さくら社



無料の学習プリント 小学3年生の算数 円 みそにゃch



コンパスを使った作図のポイント 小学3年円と球 おうちedu 家庭学習 リビング学習



円と球 どうすればお宝の場所がわかるだろうか 館山市立北条小学校 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
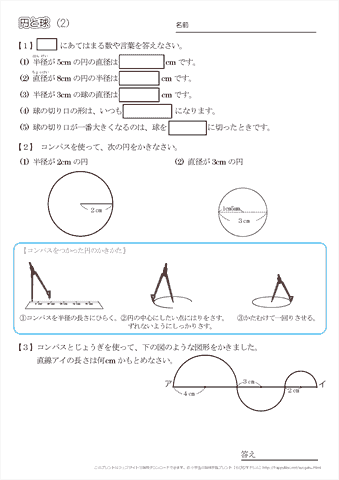



小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生




三年生 円と球 見る力の弱い児童 Noriko アカンパニスト



Www City Ota Tokyo Jp Kyouiku Topics 0525sansuu Files 25 3kaisetsu Pdf




Newton 図形に強くなる 身近な円と球 By 科学雑誌newton



0 件のコメント:
コメントを投稿